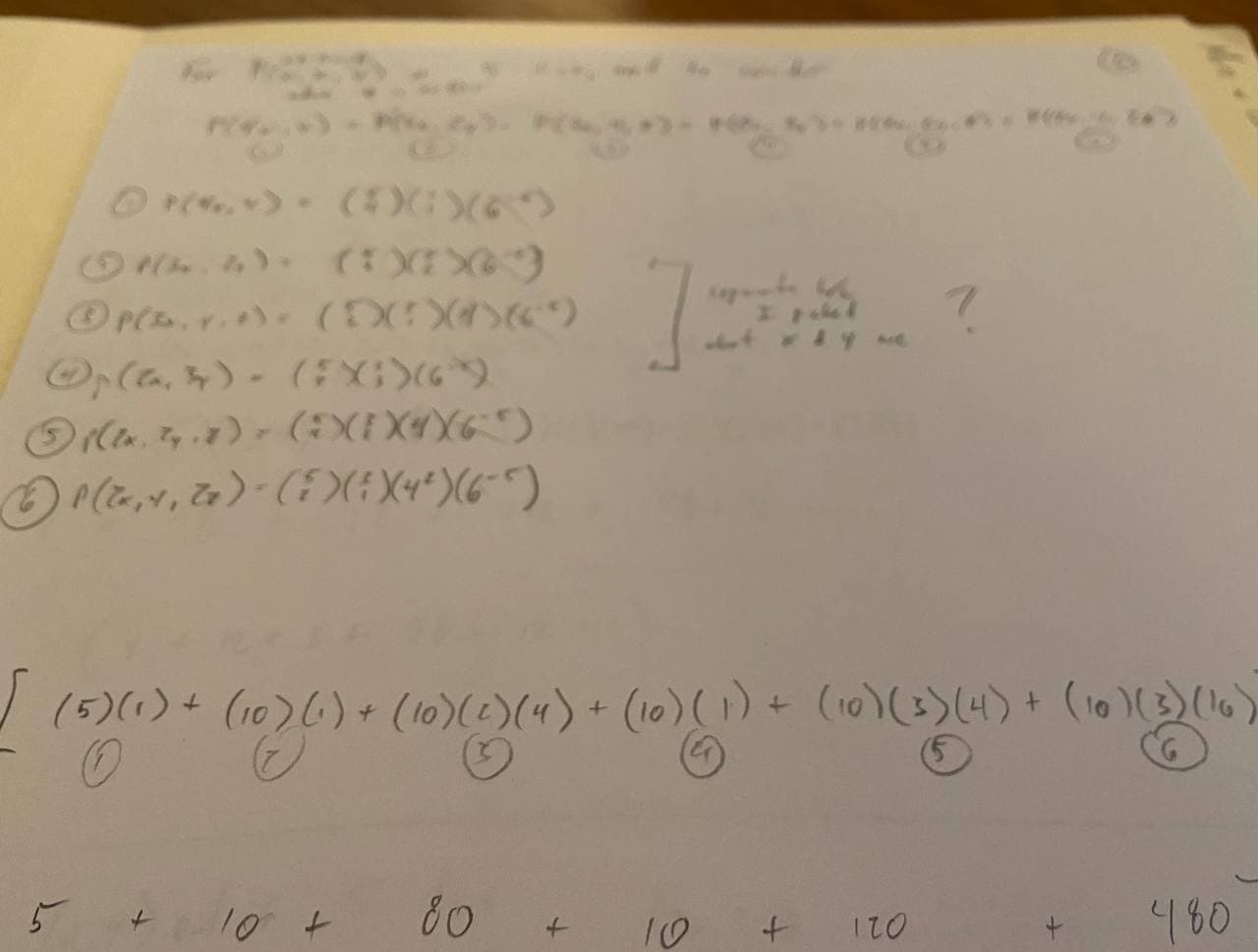Until last week, Untitled Dice Drafting Game had a title, and it was very cute because my toddler had invented it, and he is the best (and, I will emphasize, cutest) of all rhymers of words and nonwords resembling English. UNFORTUNATELY, if a toddler can come up with a name, someone else probably can too. This other game of the same name doesn’t exist, which is a bit frustrating? But it has a BGG page, and US copyright law is baffling, and anyway what’s a little rebranding among toddlers and their dads. We’re still on the hunt for an artist, anyway, and I do (almost) have a PhD in [checks notes] English.

Anyway, the crazy thing about this dice drafting game I designed (a) to have educational value for students and (b) to have entertainment value for people who like games is that I had to re-learn a bunch of math just to get it off the ground. The concept of the play itself is not complicated – dice are rolled, dice are picked, dice are used – but the grounding the theory behind the play required me to ask some weird questions in probability and combinatorics I hadn’t encountered before.

So, I knew – from that math major I earned a decade ago; yikes, am I old now? (yes) – how to calculate the probability of rolling five standard six-sided dice and getting at least three different face values on those dice. That’s a textbook question! It’s also a totally different question than how to calculate the probability of rolling five dice and getting at least a one, a two, and a three! The general question doesn’t care about which numbers you roll; the gamified question only cares about the details. If I ask my toddler to pick up a 1,2,3 and he picks up 4,5,6, I worry about my effectiveness, as a parent, in teaching him about counting. My computer? Way to go, computer! (NB: computers are less intelligent than toddlers, and much faster with calculations.)

Of course, once you know about 1,2,3 you also know about, 4,5,6 and 1,3,5 and 2,4,6 and so on. Dice don’t actually care about numbers, they only care about unique faces. So the question is specific, but the answer is general, once a specific case is handled.

I’m curious where else this overlap between specificity and generality crops up in game design. I’d assume it’s all over area control, and I’m sure there’s a parallel problem in deck-based games. Have you seen it in your own experience? Have you sensed it in any games you’ve played recently?

--Tom

[Pictured: my intial, much erased, probably incorrect stab at asking a similar question on paper, before turning to my computer to write some code.]